วิเคราะห์ปัญหาก่อนการลงทุน จำลองเสถียรภาพของสมดุลชิ้นงาน (Stability of Equilibrium)

 วิเคราะห์ปัญหาก่อนการลงทุน จำลองเสถียรภาพของสมดุลชิ้นงาน (Stability of Equilibrium)

จำลองชิ้นงานก่อนลงทุน วิเคราะห์เสถียรภาพของสมดุล

(Stability of Equilibrium)

เสถียรภาพของสมดุล (Stability of Equilibrium)

    เมื่อกล่าวถึงสภาวะสมดุลของวัตถุไม่ว่าจะอยู่นิ่งกับที่หรือเคลื่อนที่ด้วยความเร็วคงที่ก็ตาม เรามักจะเข้าใจกันแค่ว่าผลรวมของแรงและโมเมนต์ที่กระทำกับวัตถุมีค่าเท่ากับศูนย์ แต่ความเป็นจริงยังมีสิ่งที่ต้องคำนึงถึงอีกว่าสภาวะสมดุลนั้นมีเสถียรภาพด้วยหรือไม่ โดยที่เสถียรภาพของสมดุลจะมีด้วยกัน 3 ประเภท

    1. สมดุลเสถียร (Stable Equilibrium)
    2. สมดุลไม่เสถียร (Unstable Equilibrium)
    3. สมดุลสะเทิน (Neutral Equilibrium)

เพื่อให้ง่ายต่อการทำความเข้าใจขอใช้จุดศูนย์กลางมวล (Center of Mass: COM) ซึ่งแทนด้วยมวลของก้อนวัตถุ หรือ จุดศูนย์ถ่วง (Center of Gravity: CG) ซึ่งแทนด้วยน้ำหนักของก้อนวัตุที่อยู่ภายใต้แรงโน้มถ่วง มาช่วยในการอธิบาย

พิจารณากรวยตัดยอดจากรูปที่ 1 ในสภาวะที่สมดุลจะเห็นได้ว่าผลรวมของแรงมีค่าเท่ากับศูนย์และแรงจะอยู่ในแนวเดียวกันกับ CG

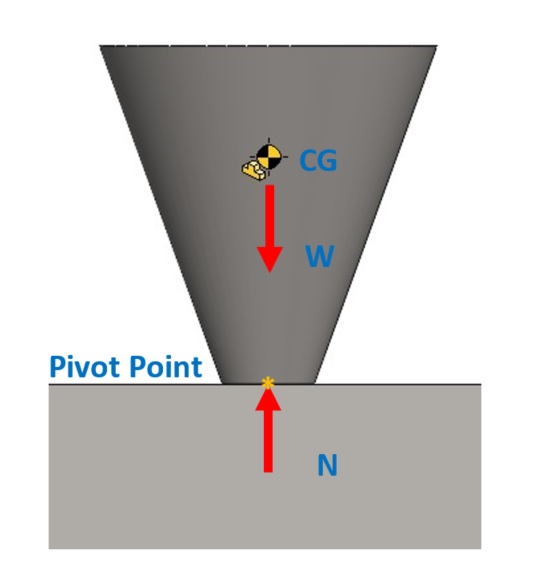
รูปที่ 1 กรวยตัดยอดในสภาวะสมดุล

เมื่อผลักให้กรวยเกิดการเอียง จากรูปที่ 2 จะเห็นได้ว่าผลรวมของแรงยังคงมีค่าเท่ากับศูนย์ จุด CG ของวัตถุเคลื่อนที่ออกและต่ำลงจากตำแหน่งเดิมแต่ยังไม่เกินจากแนวตำแหน่งของจุดหมุน (Pivot Point) ในขณะเดียวกันก็เกิดโมเมนต์ช่วยผลักให้กรวยกลับสู่สภาวะสมดุลในตำแหน่งเดิม (Rise CG) สภาวะเช่นนี้เรียกว่า สมดุลเสถียร

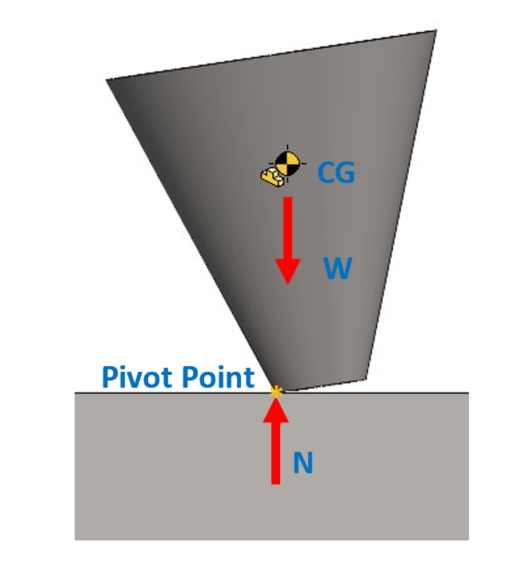
รูปที่ 2 กรวยตัดยอดในสภาวะสมดุลเสถียร

ในกรณีที่ผลักให้กรวยเอียงเพิ่มขึ้นจนจุด CG เคลื่อนที่เกินออกไปจากแนวตำแหน่งของจุดหมุน จากรูปที่ 3 แน่นอนว่าผลรวมของแรงยังคงเท่ากับศูนย์ แต่โมเมนต์ที่เกิดขึ้นแทนที่จะผลักให้กรวยกลับเข้าสู่สภาวะสมดุลในตำแหน่งเดิมแต่กลับผลักให้กรวยล้มลง (Fall CG) สภาวะเช่นนี้เรียกว่า สมดุลแบบไม่เสถียร

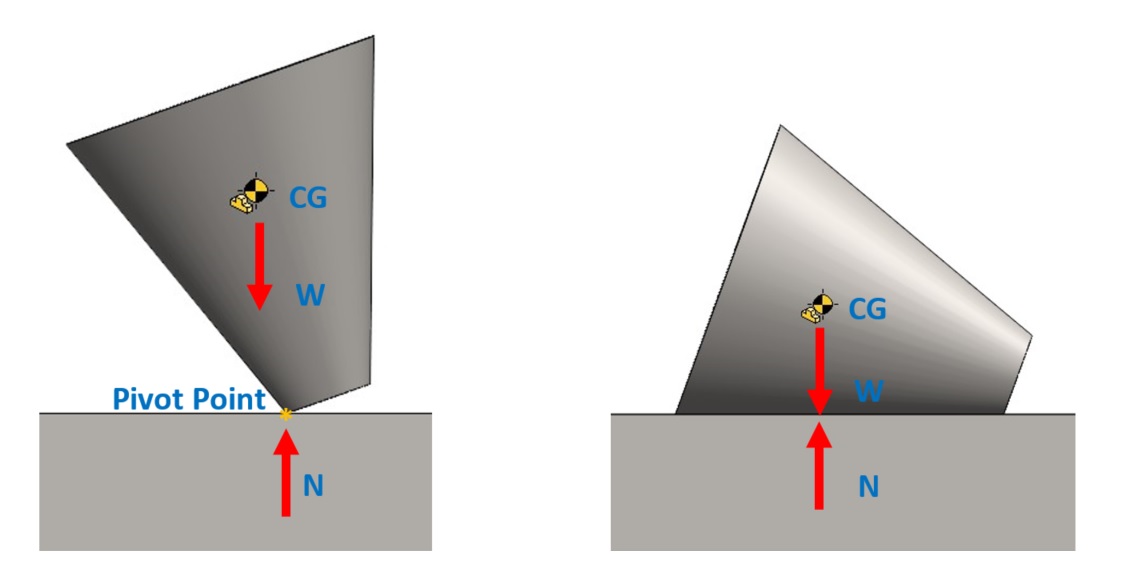
รูปที่ 3 กรวยตัดยอดในสภาวะสมดุลไม่สเถียร

กรณีสุดท้ายจะเป็นสภาวะ สมดุลแบบสะเทิน ซึ่งตำแหน่งจุด CG ของก้อนวัตถุจะไม่เปลี่ยนแปลงแม้วัตถุนั้นจะเคลื่อนที่ก็ตาม

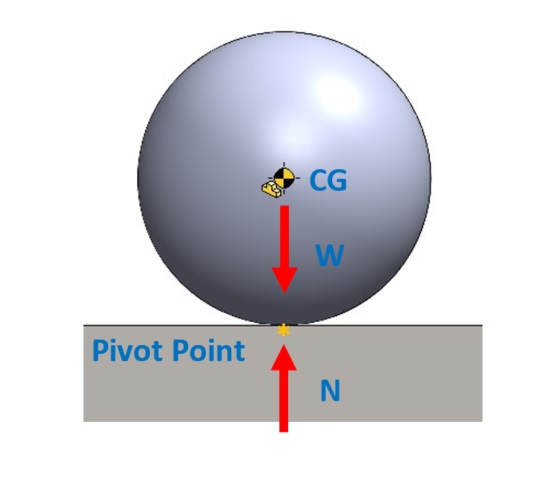
รูปที่ 4 สภาวะการสมดุลสะเทิน

จะเห็นได้ว่าวัตถุมีรูปร่างเหมือนกันก็ยังสามารถมีระยะความสูงของจุด CG ที่ต่างกันได้ ขึ้นอยู่กับว่าเราจะใช้งานมันในลักษณะใดเช่น กรณีของกรวยตัดยอด ดังรูปที่ 5

รูปที่ 5 แสดงตำแหน่งของจุด CG ในกรณีการใช้งานที่ต่างกัน

ดังนั้นพอจะสรุปได้ว่าถ้าต้องการให้วัตถุมีสภาวะที่สมดุลแบบเสถียรต้องพยายามทำดังต่อไปนี้

    1. ให้จุด CG อยู่ต่ำให้ได้มากที่สุดเท่าที่จะทำได้
    2. ให้มีระยะฐานที่กว้างที่สุดเท่าที่จะทำได้

กรณีตัวอย่างของเรื่องเสถียรภาพของสมดุล

    1. รถยนต์สปอร์ตมีจุด CG ที่ต่ำและมีระยะฐานล้อที่มากกว่ารถยนต์นั่งส่วนบุคคลจึงมีเสถียรภาพของสมดุลที่ดีกว่า
    2. การทรงตัวของรถโดยสารบนทางลาดเอียงโดยเฉพาะรถโดยสารแบบสองชั้นซึ่งมักเกิดอุบัติเหตุอยู่บ่อยครั้ง จึงเป็นเหตุให้กรมขนส่งทางบกต้องออกประกาศบังคับให้รถโดยสารที่มีความสูงตั้งแต่ 3.6 เมตร ขึ้นไปต้องผ่านการทดสอบการทรงตัวโดยมีเกณฑ์ผ่านต้องไม่ต่ำกว่า 30 องศา
    3. เสถียรภาพของตู้และชั้นวางของ (มาตรฐาน มอก.1015 เล่ม 5)

รูปที่ 6 ตัวอย่างปัญหาเรื่องเสถียรภาพของสมดุล

สำหรับตัวอย่างการวิเคราะห์เสถียรภาพของสมดุลด้วย SOLIDWORKS Motion จะเป็นเรื่องการทรงตัวของรถโดยสารบนทางลาดเอียงโดยขออธิบายก่อนในเบื้องต้นว่า ลักษณะของการวิเคราะห์ปัญหาด้วย Motion Analysis จะเป็นการวิเคราะห์การเคลื่อนที่ของวัตถุแบบแข็งเกร็งโดยจะไม่ได้พิจารณาการเสียรูปที่จะเกิดขึ้น

ซึ่งหากเราสนใจเรื่องของการเสียรูปของวัตถุด้วยต้องพิจารณาใช้งานซอฟต์แวร์ FEA ในระดับสูงที่สามารถวิเคราะห์ปัญหาแบบ Explicit Dynamics ได้เช่น SIMULIA Abaqus หรือ 3DEXPERIENCE Works Simulation เป็นต้น นอกจากนี้ยังต้องอาศัยความรู้และความเชี่ยวชาญของผู้ใช้งานในระดับสูงมาก คือ ต้องมีความรู้และความเข้าใจงานด้านวิศวกรรมเป็นอย่างดีไม่ใช่แค่ใช้งานซอฟต์แวร์เป็น

แบบจำลองการทรงตัวของรถโดยสารบนทางลาดเอียงจะประกอบด้วย

1.รถโดยสาร เพื่อให้ง่ายต่อการวิเคราะห์จึง Combine ชิ้นส่วนทั้งหมดเป็นก้อนเดียว
2.พื้นที่สามารถจำลองความลาดเอียง (Mobile Platforms)
3.พื้น (Ground)

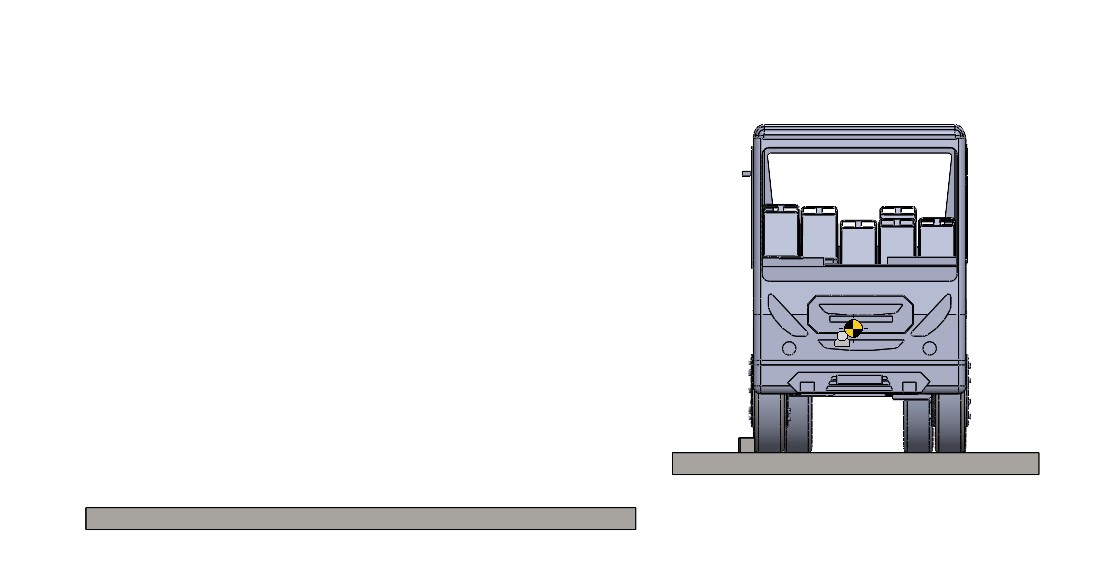
รูปที่ 7 แสดงแบบจำลองสำหรับการวิเคราะห์การทรงตัวของรถโดยสารบนทางลาดเอียง

ก่อนทำการวิเคราะห์ให้ทำการจำกัดการเคลื่อนที่ของวัตถุก่อน โดยให้ยึด (Fix) พื้นไว้ ส่วนตัวรถโดยสารและพื้นลาดเอียงจะกำหนดเป็น Float เพื่อให้พื้นลาดเอียงสามารถเคลื่อนที่ในแบบที่ต้องการ ให้ทำการสร้างสก็ตซ์แล้วทำการเมทแบบ Coincident เอาไว้

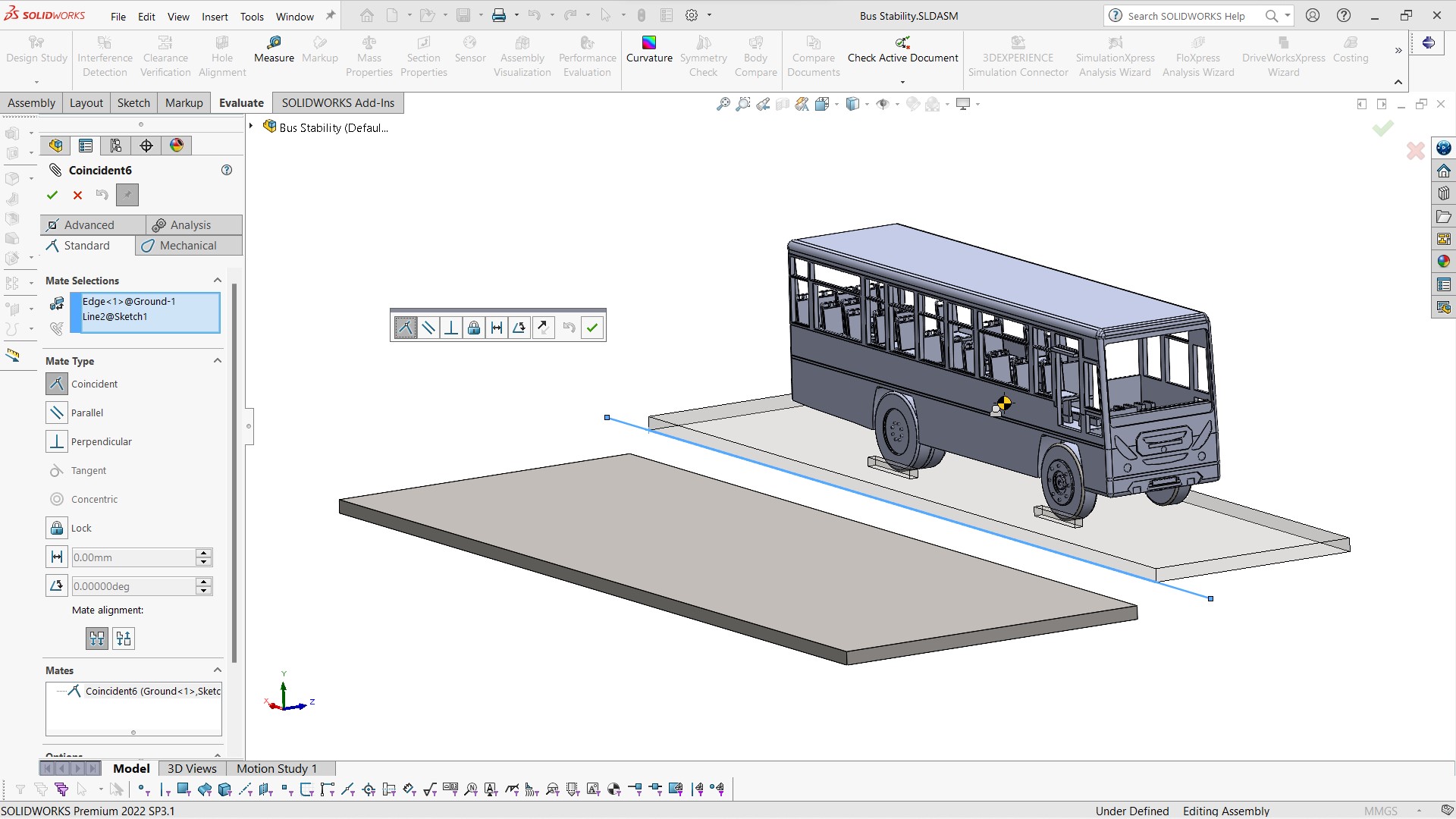
รูปที่ 8 แสดงการเมทพื้นลาดเอียงกับเส้นสเก็ตซ์

สำหรับตำแหน่งของ COM หรือ CG ปกติเราสามารถทราบได้จากคำสั่ง Mass Properties แต่หากต้องการให้ซอฟต์แวร์แสดงตำแหน่งของจุด CG ก็สามารถทำได้ โดยความสามารถดังกล่าวจะมีอยู่ใน SOLIDWORKS Premium

น้ำหนักของวัตถุแต่ละก้อน อาจกำหนดผ่านวัสดุที่กำหนดให้แก่วัตถุแต่ละก้อนโดยจะคำนวณจากความหนาแน่นของวัสดุ หรือ อาจจะใช้เป็นลักษณะ Override Mass Properties ก็ได้

การเซ็ตอัพ Motion Analysis

การกำหนดเรื่องของคอนแทคโดยในตัวอย่างจะกำหนดเป็น Steel (Dry) – Steel (Dry)

รูปที่ 9 การกำหนดเงื่อนไขคอนแทค

การกำหนดทิศทางของแรงโน้มถ่วงให้สัมพันธ์กับการเตรียมแบบจำลอง

รูปที่ 10 การกำหนดแรงโน้มถ่วง

การกำหนดการเคลื่อนที่ของพื้นลาดเอียง โดยกรมการขนส่งทางบกกำหนดให้ใช้ความเร็ว 0.05 องศา/วินาที เพราะฉะนั้นใช้เวลา 10 นาที พื้นจะลาดเอียง 30 องศา (ตัวอย่างจะกำหนดให้เคลื่อนที่ 45 องศา ภายในเวลา 15 นาที)

รูปที่ 11 การกำหนดการเคลื่อนที่ของพื้นลาดเอียง

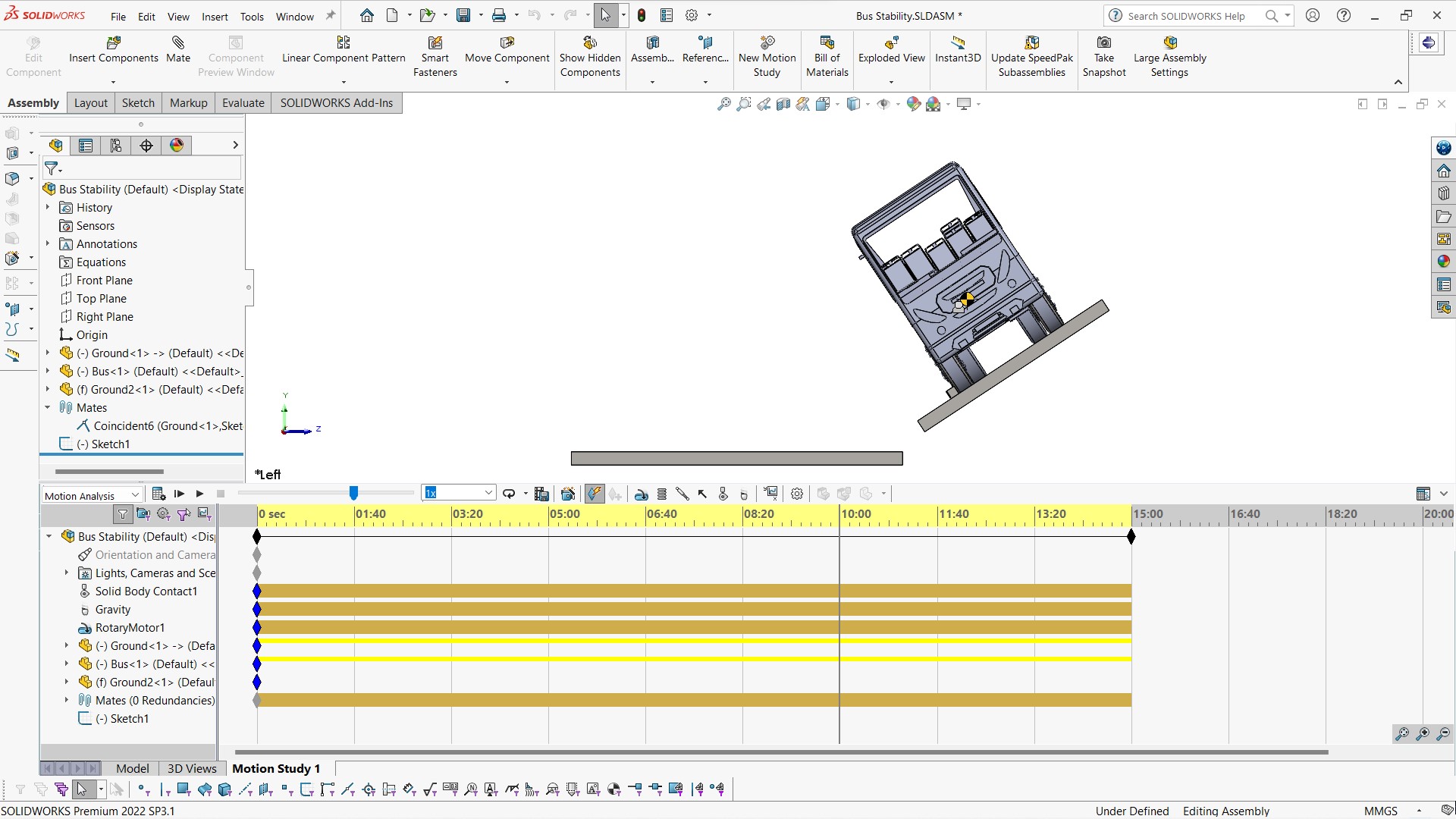
รูปที่ 12 แสดงรายละเอียดการเซ็ตอัพ และ ผลของ Motion Analysis ที่เวลา 10 นาที (30 องศา)

รูปที่ 13 แสดงผลของ Motion Analysis ที่เวลา 11:05 นาที (33.25องศา)

ทั้งหมดที่ได้อธิบายไปน่าจะเป็นประโยชน์ให้ผู้ที่สนใจนำไปประยุกต์ใช้ในเบื้องต้นกับงานที่ท่านรับผิดชอบอยู่ได้เป็นอย่างดี ก็ขึ้นอยู่กับการพิจารณาของแต่ละองค์กรว่าเพียงพอต่อการใช้งานหรือไม่ ก่อนที่จะตัดสินใจลงทุนในการวิเคราะห์ปัญหาในแบบที่ยากและซับซ้อนกว่านี้

swhotline